Зміст:
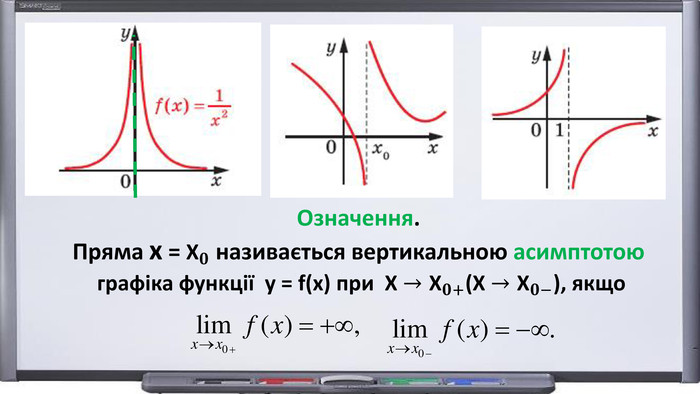
Асимптоти – це геометричні об’єкти, які визначаються шляхом розміщення функції в безкінечності. Вони використовуються для аналізу та розуміння поведінки функцій у великих та далеких значеннях. Однак, не всі функції мають асимптоти. На це можуть впливати різні причини.
Причиною відсутності асимптот може бути особливе поведінка функції в безкінечності. Наприклад, якщо функція має нескінчену кількість вершин або точок розриву, то вона не може мати асимптот. Такі особливості у формулі функції можуть бути причиною того, що її поведінка не може бути описана простою прямою або кривою.
Наприклад: функція f(x) = sin(1/x) має безліч точок розриву, тому не має асимптот.
Іншою причиною відсутності асимптот може бути незадовільна розмежуваність функцій. Якщо функція дуже швидко змінюється у великих значеннях аргументу, то асимптота може бути неможливо визначити. Наприклад, функція, яка має дуже стрімкий зріст або спад, може не мати асимптот, оскільки немає сталого нахилу, який би визначав її поведінку на великих відрізках.
Недиференційованість функцій
Але існують випадки, коли в деяких точках функція не є диференційованою. Це стається, наприклад, коли функція має розриви або “кути” у своєму графіку. У таких точках похідна функції не існує і, відповідно, функція недиференційована.
Недиференційованість функцій також може бути пов’язана з існуванням вертикальних асимптот. У цих точках функція розривається і, відповідно, не диференційована. Вертикальні асимптоти можуть формуватися, наприклад, коли функція має нульове значення в знаменнику, або коли функція росте (або спада) необмежено при наближенні до певної точки.
Також треба зазначити, що деякі функції можуть бути диференційовані збоку, але не диференційовані в середині свого проміжку. Наприклад, функція модуля abs(x) є диференційованою зліва та зправа від точки x=0, але в самій цій точці не має похідної. Такі випадки також призводять до недиференційованості функцій.
Таким чином, недиференційованість функцій є однією з причин, що можуть пояснювати відсутність асимптот у їх графіках. Вона може виникати через розриви або кути у графіку функцій, наявність вертикальних асимптот, а також несиметричну диференційованість функцій з різних боків точки.
Обмеженість функцій
Функція може бути обмеженою зверху, коли всі значення функції менші або рівні певному константному числу. Наприклад, функція f(x) = sin(x) має обмеженість зверху, оскільки значення sin(x) не перевищують 1.
Функція може бути обмеженою знизу, коли всі значення функції більші або рівні певному константному числу. Наприклад, функція g(x) = 2x + 3 має обмеженість знизу, оскільки значення 2x + 3 більші або рівні 3.
Функція може бути обмеженою з обох боків, коли всі значення функції знаходяться в певному діапазоні. Наприклад, функція h(x) = x^2 має обмеженість зверху і знизу, оскільки всі значення x^2 знаходяться в діапазоні [0, +∞).
Обмеженість функцій є важливим поняттям в математиці, оскільки воно дозволяє встановити корисні властивості функцій, такі як межі і похідні. Знання обмеженості функцій допомагає в розв’язанні математичних задач і використовується у багатьох галузях, включаючи фізику, економіку та інженерію.
Відсутність границі функції на нескінченності
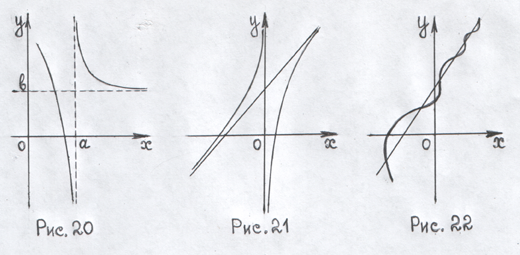
У математиці існують функції, які не мають границі на нескінченності. Це означає, що при збільшенні значень аргументу функція може набувати дуже великих або дуже малих значень, але не сходитися до певної конкретної величини. Такі функції вважаються безкінечними.
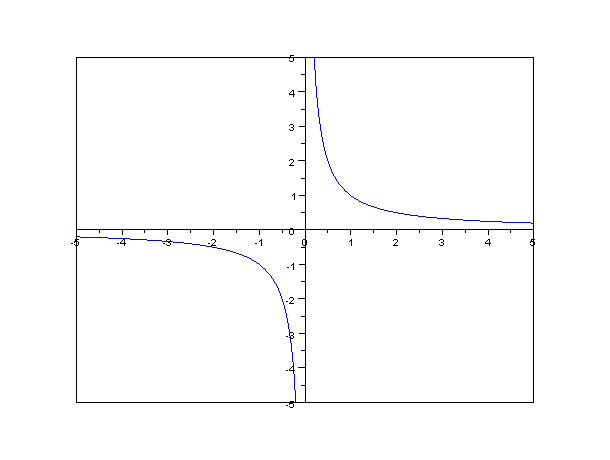
Одним з прикладів функцій, що не мають границі на нескінченності, є функція f(x) = 1/x. При зростанні значень аргументу x до додатньої нескінченності, значення функції будуть дедалі менші, а при зростанні до від’ємної нескінченності – дедалі більші. Таким чином, функція не має границі на нескінченності.
Іншим прикладом безкінечної функції може слугувати f(x) = sin(x). У цьому випадку, при зростанні значень аргументу x до нескінченності, значення функції будуть коливатися від -1 до 1, не сходячись до жодного конкретного числа.
Деякі функції можуть мати нескінченну границю на одному боці нескінченності і відсутню границю на іншому боці. Наприклад, f(x) = sin(x)/x. При зростанні значень аргументу x до додатньої нескінченності, значення функції будуть збігатися до нуля, тобто мати границю, але при зростанні до від’ємної нескінченності, значення будуть дедалі більшими і не будуть збігатися до жодного конкретного числа, тобто границі не існує.
Відсутність границі функції на нескінченності є важливою властивістю, яка може впливати на поведінку та властивості функції в різних контекстах аналізу.
Неперервність функцій

У математиці поняття неперервності функцій відіграє важливу роль при дослідженні їх властивостей. Функція називається неперервною, якщо вона зберігає свої значення при невеликих змінах аргументу.
Існує декілька видів неперервності функцій:
- Функція називається неперервною в точці x_0, якщо для будь-якого числа ε > 0 існує число δ > 0 таке, що для будь-якого числа x з відрізка (∞, −∞) виконується нерівність |x – x_0| < δ → |f(x) – f(x_0)| < ε.
- Функція називається неперервною на відрізку [a, b], якщо вона неперервна в кожній точці цього відрізку.
- Функція називається неперервною зліва в точці x_0, якщо для будь-якого числа ε > 0 існує число δ > 0 таке, що для будь-якого числа x з відрізка (x_0 – δ, x_0) виконується нерівність |x – x_0| < δ → |f(x) – f(x_0)| < ε.
- Функція називається неперервною справа в точці x_0, якщо для будь-якого числа ε > 0 існує число δ > 0 таке, що для будь-якого числа x з відрізка (x_0, x_0 + δ) виконується нерівність |x – x_0| < δ → |f(x) – f(x_0)| < ε.
Неперервність функцій є важливою характеристикою, оскільки вона гарантує наявність асимптоти та інших властивостей функції. Тому вивчення цього поняття важливо при розв’язанні різноманітних задач та дослідженні функцій.